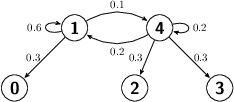
The Markov chain given in the question has two transient states and one recurrent state.
The recurrent state is state 2 and as such the matrix has already been arranged in the
required form for this type of problem; namely:
\begin{equation}
P = \left(
\begin{matrix}
Q & R \\
0 & I
\end{matrix}
\right)
\nonumber
\end{equation}
with $Q$ connecting the transient states to the transient states and $R$ connecting the transient
states to the recurrent states. In this question we thus have:
$$
\mathbf{Q} = \left(
\begin{matrix}
0.6 & 0.1 \\
0.2 & 0.2
\end{matrix}
\right)
\qquad \textrm{and} \qquad
\mathbf{R} = \left(
\begin{matrix}
0.3
0.6
\end{matrix}
\right)
$$
To calculate the vector of hitting times, $\mathbf{h}$, for this chain we need to use:
$$
\mathbf{h} = ( \mathbf{I} - \mathbf{Q} )^{-1}\mathbf{1}
$$
and as such we need to invert a $2\times2$ matrix as shown below:
$$
( I - Q )^{-1} =
\left(
\begin{matrix}
0.4 & -0.1 \\
-0.2 & 0.8
\end{matrix}
\right)^{-1} = \frac{1}{ 0.4\times0.8 - 0.1 \times 0.2 } \left(
\begin{matrix}
0.8 & 0.1 \\
0.2 & 0.4
\end{matrix}
\right) =
\left(
\begin{matrix}
8/3 & 1/3 \\
2/3 & 4/3
\end{matrix}
\right)
$$
When this matrix is multiplied by a vector containing all ones we get the desired vector of hitting times:
$$
\mathbf{h} = ( \mathbf{I} - \mathbf{Q} )^{-1} \mathbf{1} =
\left(
\begin{matrix}
8/3 & 1/3 \\
2/3 & 4/3
\end{matrix}
\right)
\left(
\begin{matrix}
1 \\
1
\end{matrix}
\right) =
\left(
\begin{matrix}
3 \\
2
\end{matrix}
\right)
$$
Now, obviously, calculating the hitting probabilities using:
$$
\mathbf{H} = ( \mathbf{I} - \mathbf{Q} )^{-1}\mathbf{R}
$$
is pointless because there is only one recurrent (absorbing) state. Lets do
it anyway, however, in order to confirm that the formula above gives a result
that is in accordance with our intuition.
$$
\mathbf{H} = ( \mathbf{I} - \mathbf{Q} )^{-1} \mathbf{R} =
\left(
\begin{matrix}
8/3 & 1/3 \\
2/3 & 4/3
\end{matrix}
\right)
\left(
\begin{matrix}
0.3 \\
0.6
\end{matrix}
\right) =
\left(
\begin{matrix}
4/5 + 1/5 \\
1/5 + 4/5
\end{matrix}
\right) =
\left(
\begin{matrix}
1 \\
1
\end{matrix}
\right)
$$