Markov chains in continuous times : Exercises
Introduction
Example problems
Click on the problems to reveal the solution
Problem 1
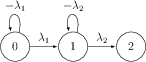
Problem 2

Problem 3
We can use these three probabilities to calculate the total mass of the sample at time $t$ by calculating the expected mass and multiplying it by the number of atoms that are present in the sample, which will not change. Only the types of atoms that are present will change: \[ \begin{aligned} \mathbb{E}[M(t)] = & N( 220 P_{00}(t) + 216 P_{01}(t) + 212 P_{02}(t) ) \\ = & N \left[ 220 e^{-\lambda_1 t} + 216 \frac{\lambda_1}{\lambda_2 - \lambda_1} \left( e^{-\lambda_1 t} - e^{-\lambda_2 t} \right) + 212\left( 1 - e^{-\lambda_1 t} - \frac{\lambda_1}{\lambda_2 - \lambda_1} \left( e^{-\lambda_1 t} - e^{-\lambda_2 t} \right) \right) \right] \\ =& N\left[ 212 + 8e^{-\lambda_1 t} + 4 \frac{\lambda_1}{\lambda_2 - \lambda_1} \left( e^{-\lambda_1 t} - e^{-\lambda_2 t} \right) \right] \end{aligned} \]
