The Chapman Kolmogorov Relation : Exercises

Introduction

When you have completed the following problems you should be able to do three things with Markov chains: (1) identify the problems where the Chapman-Kolmogorov relation is required to calculate probabilities, (2) identify the problems where the Chapman-Kolmogorov relation is innapropriate and (3) solve both these types of problem.

Example problems

Click on the problems to reveal the solution

Problem 1

Consider the sequence of bases/nucleotides/letters of a strand of DNA (T, A, C, G) to be the states, $ X \in \{0,1,2,3\} $ respectively, of a Markov chain. The letters are abbreviations for Thymine, Adenine, Cytosine and Guanine. Suppose the chain is described by the transition matrix: $$ \left( \begin{matrix} 0.2 & 0.3 & 0.3 & 0.2 \\ 0.2 & 0.3 & 0.3 & 0.2 \\ 0.2 & 0.3 & 0.2 & 0.3 \\ 0.2 & 0.2 & 0.3 & 0.3 \\ \end{matrix} \right) $$ Calculate the probability of the following sequences: AGT, GTCC, CGGT. You may assume the first letter in the sequence is given (has probability 1).

We can use the information given in the transition matrix and the fact that the probability of the first letter is equal to one to find the probabilities required by this question directly as shown below. $$ \begin{aligned} P(AGT) & = p_{13}p_{30} = 0.2 \times 0.2 = 0.04 \\ P(GTCC) & = p_{30}p_{02} p_{22} = 0.2 \times 0.3 \times 0.2 = 0.012 \\ P(CGGT) & = p_{23}p_{33}p_{30} = 0.3 \times 0.3 \times 0.2 = 0.018 \end{aligned} $$

Problem 2

Consider a Markov chain with two states $X \in \{0, 1\}$. The transition matrix has the form: $$ P= \left( \begin{matrix} \frac{1}{3} & \ \ & \frac{2}{3} \\ & & \\ \frac{1}{2} & \ \ & \frac{1}{2} \\ \end{matrix} \right) \qquad . $$ Calculate the following transition probabilities: $$ P (X_1 = 1 |X_0 = 0) \qquad P (X_2 = 0|X_0 = 1) \qquad P (X_3 = 0 |X_0 = 0) $$

We can use the information contained in the transition matrix to "calculate" the first of these probabilities directly as shown below: $$ \begin{aligned} P(X_1 = 1 |X_0 = 0) & = \frac{2}{3} \\ \end{aligned} $$ For the second we need to use the Chapmann-Kolmogorov relation so we need to calculate the 2nd power of the matrix: $$ \left( \begin{matrix} \frac{1}{3} & \frac{2}{3} \\ \frac{1}{2} & \frac{1}{2} \end{matrix} \right) \left( \begin{matrix} \frac{1}{3} & \frac{2}{3} \\ \frac{1}{2} & \frac{1}{2} \end{matrix} \right) = \left( \begin{matrix} \frac{4}{9} & \frac{5}{9} \\ \frac{5}{12} & \frac{7}{12} \end{matrix} \right) $$ So $P (X_2 = 0|X_0 = 1)=\frac{5}{12}$

For part (iii) we have to calculate the third power of the matrix $$ \left( \begin{matrix} \frac{1}{3} & \frac{2}{3} \\ \frac{1}{2} & \frac{1}{2} \end{matrix} \right) \left( \begin{matrix} \frac{4}{9} & \frac{5}{9} \\ \frac{5}{12} & \frac{7}{12} \end{matrix} \right) = \left( \begin{matrix} \frac{23}{54} & \frac{31}{54} \\ \frac{31}{72} & \frac{41}{72} \end{matrix} \right) $$ For part (iii) we thus have $P (X_3 = 0 |X_0 = 0)=\frac{23}{54}$

Problem 3

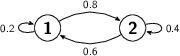
Consider a Markov chain between two states, $X=0$ and $X=1$, for which the transition matrix is given by: $$ P= \left( \begin{matrix} 0.2 & 0.8 \\ 0.6 & 0.4 \\ \end{matrix} \right) \qquad . $$ Draw the transition diagram (graph) for this chain and then calculate the following transition probabilities: $$ P(X_{1}=0 \vert X_{0}=0) \quad , \quad P(X_{2}=0 \vert X_{0}=1) \quad , \quad P(X_{3}=1 \vert X_{1}=1) \qquad . $$ Lastly, given that $X_{0}=0$, calculate the probability of the chain (sequence) $00101$ for $X_0,X_{1},X_{2},X_{3},X_{4}$,

The transition graph is as shown below:

The probabilities required are equal to: $$ P(X_{1}=0 \vert X_{0}=0) = 0.2 \qquad P(X_{2}=0 \vert X_{0}=1) = 0.36 \qquad P(X_{3}=1 \vert X_{1}=1) = 0.64 $$ And if $X_0=0$ then: $$ P( X_1=0 \wedge X_2=0 \wedge X_3=1 \wedge X_4=0 \wedge X_5=1 ) = 0.0768 $$

Problem 4

Suppose the autumn weather in Belfast, from day to day, follows a Markov process. If it is raining here today, there is a probability 0.3 that it will rain again tomorrow. Similarly, the probabilities of cloudy weather (with no rain) or sunshine the next day are 0.5 and 0.2, respectively. We can summarize all the transition probabilities between the states (that is the weather from one day to the next) $X \in \{ R,C,S \}$, in the transition matrix: $$ P= \left( \begin{matrix} 0.3 & 0.5 & 0.2 \\ 0.3 & 0.4 & 0.3 \\ 0.2 & 0.5 & 0.3 \\ \end{matrix} \right) \qquad . $$ Today is a Friday in Belfast, in mid-October, and it is raining. Use the information above to calculate the probability that both the next two days, Saturday and Sunday, will be sunny and to calculate the probability of rain on Sunday. Can you suggest one (or more) aspects of this model that is unrealistic and how we might thus improve the model?

$$ P(\textrm{next two days sunny}) = 0.06 \qquad P(\textrm{rain on Sunday}) = 0.28 $$

In terms of the improvments to the model we could think about any of the following:

There are weather variations within the days.
Weather is predictable one day ahead this model assumes it is random
Seasonal variations are not taken into account. To incorporate this correctly we would need to use an inhomogeneous Markov chain

Problem 5

Marital status for a man in his 30s is considered using the following Markov process. The state space of the process consists of three states: Single ($X=0$), Cohabiting ($X=1$), Married ($X=2$). The transition matrix from year to year has the following form: $$ P= \left( \begin{matrix} 0.60 & 0.35 & 0.05 \\ 0.20 & 0.70 & 0.10 \\ 0.10 & 0.05 & 0.85 \end{matrix} \right) \qquad . $$ Draw the transition graph for this Markov chain and then answer the following questions:

Calculate the probability that a 35-year-old married man gets divorced next year, and marries again the following year.

Given a 30-year-old man is single this year, calculate the the probability that he will still be single in two years time.

Do you think this is a good model for the marital status of a man? What is good/bad about it?

Transition graph:

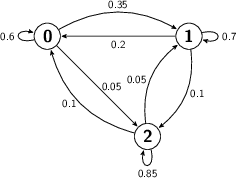
Probablity that he gets divorsed and then remaires in two years: $P = 0.01$
Probability single 30-year will still be single in two years: $P= 0.435$

This is not a good model as the assumption of Markovianity is dubious. For instance a man who has cohabited with his partner for many years is more likely to get married than a man who has cohabitted for only one year.